自瞄算法使用说明(理论篇)
发布于 2024-04-05 2519 次阅读
发布于 2024-04-05 2519 次阅读
在 RoboMaster 比赛中,机器人需要精准的命中敌方机器人身上搭载的四块装甲板才能造成有效伤害,这就需要我们精准的获取目标装甲板的位置用于计算发射时的云台姿态。在比赛中,有两种不同的装甲模块,大型装甲板(230mm*127mm)和小型装甲板(135mm*125mm)。它们都贴有数字标签(从 1 到 5)以及一些特殊图案,并且在装甲模块的边缘有两个灯条,灯条的灯光可以是红色或蓝色。当己方为红队时,机器人上的灯光将是红色的,目标机器人上的灯光将是蓝色的。同时装甲模块上的数字标签用于区分不同的机器人。不同的机器人在装甲模块上有不同的数字标签。同时由于比赛中发射的是塑胶弹丸,弹速一般为 15~30m/s,会在出膛后有一定的飞行时间,因此估计出目标的速度进行目标的预测是非常有必要的。

如图所示没有预测时的效果:
在左图状态下发射一枚弹丸,当弹丸到达目标在发射时的位置时,目标已经离开了瞄准的位置。
总的来说,想要在比赛中实现良好的自动瞄准效果,因此需要:
(1) 在图像中实时的识别目标并精准的获取目标相对己方机器人的三维位置;
(2) 较为精确的估计目标的运动状态以获得实时的预测瞄准位置。

由于需要获取目标相对己方机器人的三维位置才可计算出弹丸发射时的云台姿
态,因此需要使用三维重建算法。
选用最方法:通过单目 PnP 从单张图像中恢复物体的三维位置姿态。该方法只需要RGB 图像即可获取目标的位置姿态,而一般工业相机都可以提供高帧率的 RGB 图像,还可根据不同机器人识别距离的需求更换不同焦距的镜头,可以说PnP是不二之选。
采用神经网络推理出装甲板的四点和openvino加速推理。
选用神经网络的原因:
有可能带来的影响:
由于图像中会同时出现多个目标,在自动瞄准时云台应该保持持续锁定同一目标,所以跟踪算法是非常有必要的。跟踪算法主要有基于图像信息的 KCF 跟踪算法,是一种基于核相关滤波的目标跟踪算法,它是在 CSK 算法的基础上进行了改进,提高了跟踪的准确度和鲁棒性,以及使用卡尔曼滤波器对每个目标的状态进行预测和更新同时仅使用 IoU 作为数据关联的指标的多目标跟踪算法 SORT等。考虑到对于实时性的要求以及在该自动瞄准任务中,目标的图像特征都十分相似,KCF 不适合用于该任务的跟踪,故选用 SORT 算法中对于目标滤波及关联的处理思路作为单目标跟踪器的算法基底。
前面提到需要对于运动目标有一定的预测,这需要我们对于目标的运动状态(例如目标的运动速度)有一定的估计,而除位置姿态外其他的状态是无法直接被系统所观测的,这就需要状态估计器来从观测数据来推断系统状态。
考虑到在 RoboMaster 比赛中,目标机器人为了规避弹丸的击打,运动状态一般为旋转运动叠加平移运动,而观测的对象为目标机器人上所搭载的装甲板,为了获取最佳的击打效果,应该估计出目标机器人的整体运动状态而非单一装甲板的运动状态,而这意味着状态空间到观测空间的转换是一非线性过程,所以卡尔曼滤波是不能直接使用的。同时考虑到这一过程的非线性程度不大,再加上系统对于实时性的要求,所以采用采用扩展卡尔曼滤波作为自动瞄准系统的状态估计算法。
第一步:神经网络推理检测装甲板,根据相机内参利用PnP解算获取三维位姿。
第二步如图:

总的来说,该算法系统的输入为单目 RGB 图像以及相机的内参矩阵及镜头畸变系数,以及云台姿态信息,最终输出在惯性系下跟踪着的机器人状态,其中包含机器人中心位置及机器人的运动线速度和角速度,以及两对装甲板的相对位置关系。
考虑到比赛中的相机一般安装在云台上,并且上一步做观测的坐标系是相机坐标系,该坐标系会随着云台运动而变化,在进行目标跟踪时云台会随着目标一起运动,若在相机坐标系下做状态估计得到的速度会耦合云台自身的运动以及目标的运动,无法得到正确的目标状态,因此需要获取云台的姿态将观测的坐标系变为以云台中心为原点的惯性系。
由于在比赛时相机同一画面中经常会出现多个目标,并且同一机器人在旋转时也会出现视野中的装甲板跳变成另一块装甲板的情况,因此在自动瞄准系统中使用跟踪器是非常有必要的。
跟踪器工作流程:

跟踪器默认选择离相机光心最近的目标作为跟踪对象,选择目标后初始化扩展卡尔曼滤波器,滤波器的初值根据当前跟踪对象设𝑟为 0.2m 计算处对应的(𝑥𝑐, 𝑦𝑐 ), 𝑧𝑎, 𝜃与当前跟踪目标对象一致,速度都默认为 0。
跟踪器的更新步骤首先由扩展卡尔曼滤波器得到当前帧的预测状态,再通过观测方程ℎ(⋅)将状态空间映射到观测空间得到对应的预测装甲板位置,根据然后遍历当前帧中的目标位置与预测位置进行匹配,若当前帧不存在目标或所有目标位置与扩展卡尔曼滤波器的预测位置的偏差都过大则认为目标丢失,重置扩展卡尔曼滤波器。最后选取位置相差最小的目标作为最佳匹配项作为观测量更新扩展卡尔曼滤波器。
为了避免识别器出现误识别以及目标短暂丢失时跟踪器保持跟踪,跟踪器共设计了四个状态,其中状态转换过程如图:
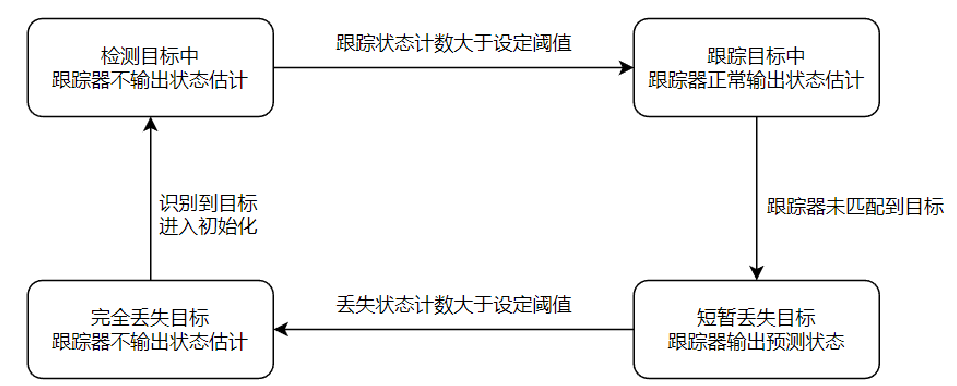
只有当跟踪器为“跟踪目标中”状态时才会输出更新后的估计状态,而当跟踪器为“短暂丢失目标”状态时会输出预测的状态,有效避免了出现一帧误识别时云台错误响应,同时当目标短暂丢失时机器人云台仍然能够保持跟踪。

比赛中各参赛队为了规避击打,机器人自身底盘运动往往不是单纯的平移运动而是旋转与平移的叠加,因此采用常规的匀速直线运动模型对装甲板做状态估计效果不佳。且四块装甲板与机器人中心在 XOY 平面上的运动学关系如上图所示,用公式表达为:

观测的装甲板位姿和机器人整体底盘状态可以由上式联系在一起,并且该状态空间与观测空间的变换是非线性的,使用扩展卡尔曼滤波对机器人的整体状态做状态估计。
扩展卡尔曼滤波(Extended Kalman Filter,EKF)是一种针对非线性系统的状态估计方法,它是在卡尔曼滤波(Kalman Filter,KF)的基础上进行的改进。
卡尔曼滤波是一种利用线性系统的状态方程和观测方程,结合贝叶斯理论和最小均方误差原则,通过预测和更新两个步骤来递推地估计系统状态的方法。
扩展卡尔曼滤波的主要思想是利用泰勒展开,将非线性系统在某个参考点处近似为线性系统,然后应用卡尔曼滤波的预测和更新公式来进行状态估计。
扩展卡尔曼滤波的主要步骤如下:
预测:根据非线性状态方程,利用上一时刻的状态后验估计和控制输入,预测当前时刻的状态先验估计和误差协方差矩阵。
线性化:在预测的状态先验估计处,对非线性状态方程和非线性观测方程进行一阶泰勒展开,得到相应的线性化状态转移矩阵和观测矩阵。
更新:根据非线性观测方程,利用预测的状态先验估计和观测数据,计算观测残差和卡尔曼增益,然后根据卡尔曼滤波的更新公式,得到当前时刻的状态后验估计和误差协方差矩阵。
扩展卡尔曼滤波的优点是可以处理非线性系统,并且相比于其他非线性滤波方法,如无迹卡尔曼滤波(Unscented Kalman Filter,UKF)和粒子滤波(Particle Filter,PF),具有较低的计算复杂度和内存需求。
扩展卡尔曼滤波的缺点是对于高度非线性或多峰分布的系统,一阶泰勒展开可能不足以近似真实的系统行为,并且可能导致过度自信或发散的问题。因为当前任务状态-观测转移的非线性程度不高以及系统对于实时性有较高的要求,故扩展卡尔曼装滤波比较适合作为该任务的状态估计器。
自动瞄准任务中对于目标只有观测没有控制,所以扩展卡尔曼滤波中的输入-控制模型𝐵和控制器向量𝑢可忽略。扩展卡尔曼滤波的预测步如下:
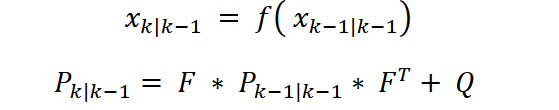
更新步为:

假设目标机器人的运动模型为底盘匀速直线运动,仅在 XOY 平面有旋转运动叠加,则 EKF的状态量𝑥为机器人的中心坐标、在 XOY 平面下的旋转角度、线速度、角速度以及机器人中心到当前观测装甲板的距离(c下标表示车辆中心,a下标表示amor,装甲板):

观测量𝑧为惯性系下的装甲板位置以及在 XOY 平面下的旋转角度:

状态转移方程组𝑓(⋅)是线性的:
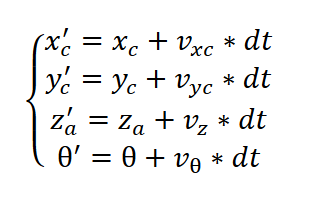
状态转移矩阵𝐹为:

根据方程:

可以得到观测方程组ℎ(⋅)为:

由方程组ℎ(⋅)求得雅可比矩阵𝐽ℎ为:

最后,根据实际观测的噪声情况设置𝑅矩阵,根据系统运行的频率及观测的准确性设置𝑄矩阵,即可获得良好的效果。
同一机器人有四块装甲板,在对其中一块装甲板跟踪时若目标机器人在旋转,就会出现 ID 相同但实际上不是跟踪着的目标的装甲板,如图示另一对装甲板的情况,需要在装甲板跳变时对扩展卡尔曼滤波器进行一定的处理。

在目标机器人旋转时发生装甲板跳变,则对应着扩展卡尔曼滤波器状态量中的𝑧𝑎, θ, 𝑟发生了跳变,但状态量中的中心位置以及线速度,角速度并没有突变,处理方式为使用滤波器外的一个变量 z2 存下滤波器状态量中的𝑧𝑎,并根据观测到的跳变装甲板信息修改𝑧𝑎, θ。注意到上图所示另一对装甲板与中心也有一个固定的距离关系,所以此时还需要另一个变量 r2 与滤波器状态量中的 r 做值的交换。通过这种方式,扩展卡尔曼滤波器中的状态量就变成了机器人中心状态与跳变后装甲板的关系。
至此,结合扩展卡尔曼滤波器的状态量以及变量 z2,r2,即可根据假设的运动情况推导出目标在一段时间后的目标中心位置,进而可以推断出对应的四块装甲板位置。通过对四块装甲板的简单选择后计算对应的云台姿态并进行控制,就可以实现对旋转平移的敌方机器人实现精准的击打。
Comments | NOTHING